Matlab求解非线性规划,fmincon函数的用法总结
1.简介
在matlab中,fmincon函数可以求解带约束的非线性多变量函数(Constrained nonlinear multivariable function)的最小值,即可以用来求解非线性规划问题
matlab中,非线性规划模型的写法如下

2.基本语法
[x,fval]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x的返回值是决策向量x的取值,fval的返回值是目标函数f(x)的取值
fun是用M文件定义的函数f(x),代表了(非)线性目标函数
x0是x的初始值
A,b,Aeq,beq定义了线性约束 ,如果没有线性约束,则A=[],b=[],Aeq=[],beq=[]
lb和ub是变量x的下界和上界,如果下界和上界没有约束,则lb=[],ub=[],也可以写成lb的各分量都为 -inf,ub的各分量都为inf
nonlcon是用M文件定义的非线性向量函数约束
options定义了优化参数,不填写表示使用Matlab默认的参数设置
3.实例
示例,求下列非线性规划:
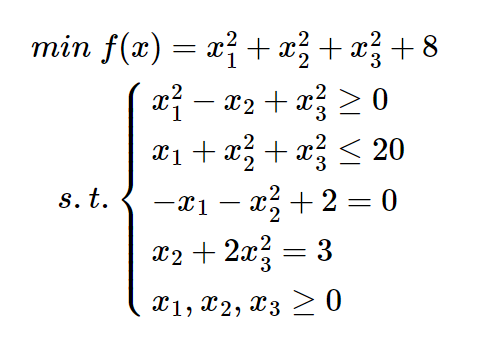
(1)编写M函数fun1.m 定义目标函数:
function f=fun1(x);
f=x(1).^2+x(2).^2+x(3).^2+8;
(2)编写M函数fun2.m定义非线性约束条件:
function [g,h]=fun2(x);
g=[-x(1).^2+x(2)-x(3).^2
x(1)+x(2).^2+x(3).^3-20];
h=[-x(1)-x(2).^2+2
x(2)+2*x(3).^2-3];
(3)编写主程序函数
[x,y]=fmincon('fun1',rand(3,1),[],[],[],[],zeros(3,1),[],'fun2')
所得结果为:x1=0.5522,x2=1.2033,x3=0.9478最小值y=10.651

|

|
