## 深度优先搜索(Depth Fiest Search)
简称 深搜或者DFS,DFS是一种图的算法,基本思想就是用计算机的强大计算力去穷举每一种可能的情况,在计算机网络和人工智能方面都有广泛应用,DFS的另一种名称叫做回溯法,就是要先改变参数进行递归,递归之后我们再返回原来的状态为下一次的递归做准备。
我们先来看个图
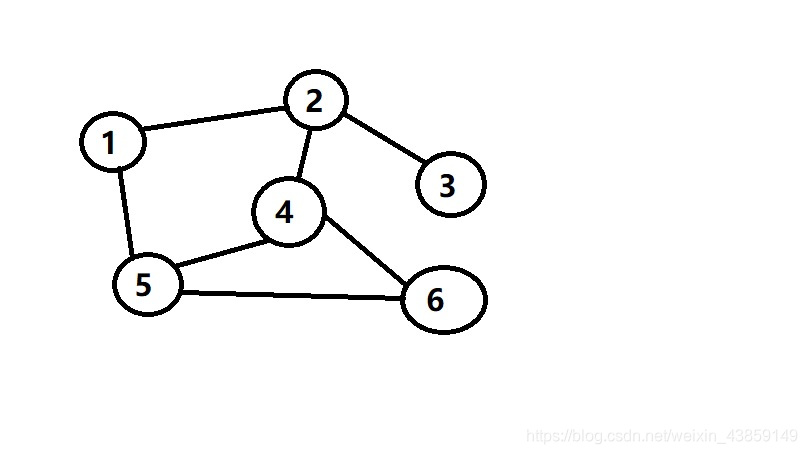 我们要用DFS来遍历这个图然后得出结果
首先我们就从1开始吧
我们要用DFS来遍历这个图然后得出结果
首先我们就从1开始吧
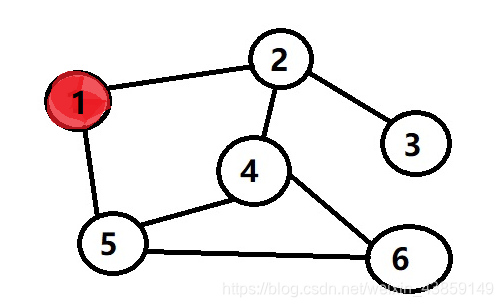 然后我们就一步一步开始搜索,这里我们可以选择2也可以选择5,最后可能顺序不一样,思路对了就行了
我这里就选择2吧
然后我们就一步一步开始搜索,这里我们可以选择2也可以选择5,最后可能顺序不一样,思路对了就行了
我这里就选择2吧
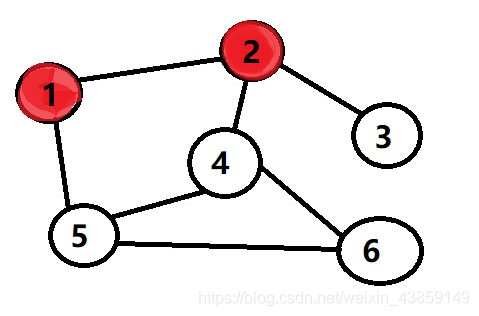 再到3
再到3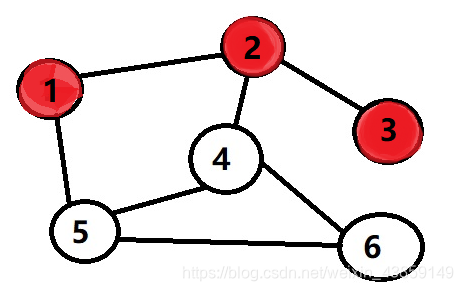 走完3之后我们发现已经到尽头了,这里我们就要用到回溯,返回到2继续搜索到4
走完3之后我们发现已经到尽头了,这里我们就要用到回溯,返回到2继续搜索到4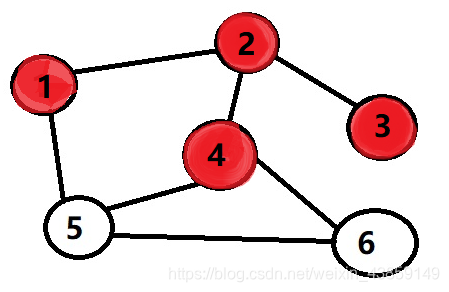 继续搜索
继续搜索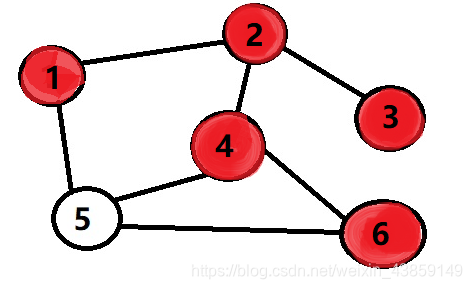
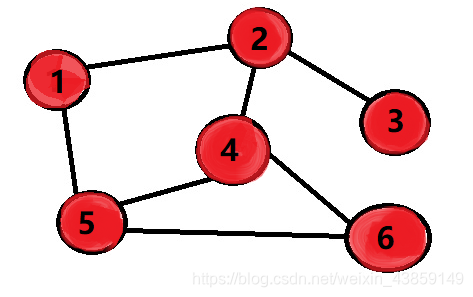 完成搜索后我们就得到了结果,1 2 3 4 6 5,通俗的讲DFS就是一条路走到黑,走不通了我们就返回去继续找能走的路
完成搜索后我们就得到了结果,1 2 3 4 6 5,通俗的讲DFS就是一条路走到黑,走不通了我们就返回去继续找能走的路
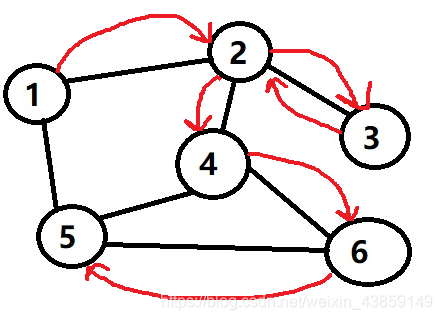 我们也可以用栈(Stack)来表示,方便理解
我们也可以用栈(Stack)来表示,方便理解
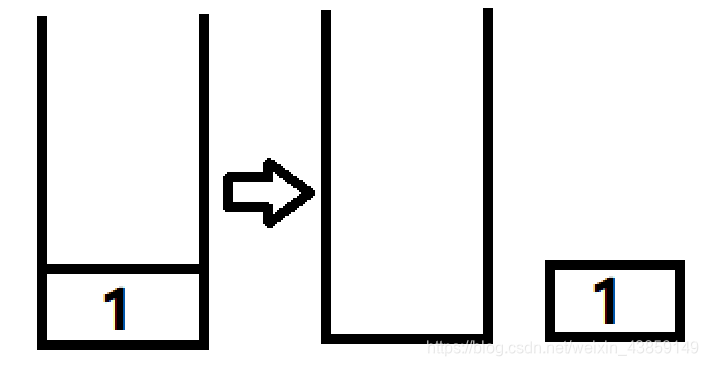 1弹出来之后我们就要把和与1向连的2和5放入栈中,然后又从栈中弹出2,
1弹出来之后我们就要把和与1向连的2和5放入栈中,然后又从栈中弹出2,
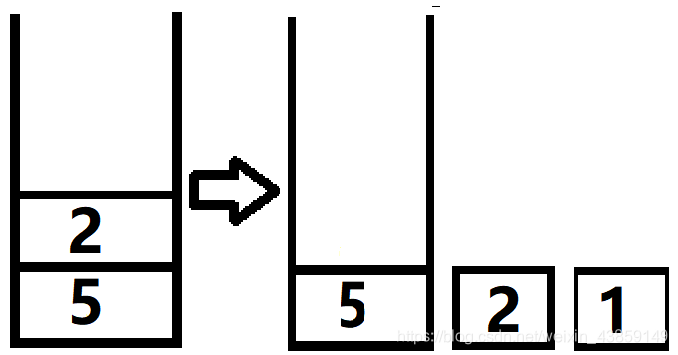 2弹出之后我们又把与2相连的3和4放入栈中,
后面也是同样的操作
2弹出之后我们又把与2相连的3和4放入栈中,
后面也是同样的操作
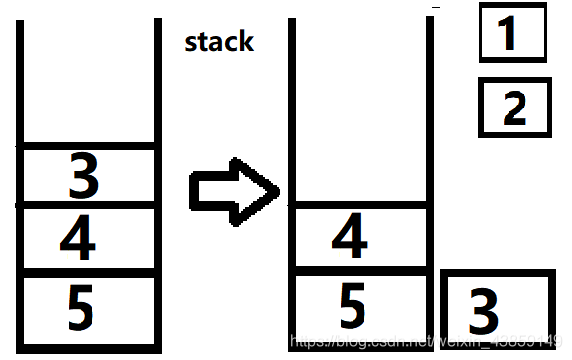 这里我们弹出3后我们发现并没有数与3相连,所以我们就不放任何数进入栈,然后继续弹出4
这里我们弹出3后我们发现并没有数与3相连,所以我们就不放任何数进入栈,然后继续弹出4
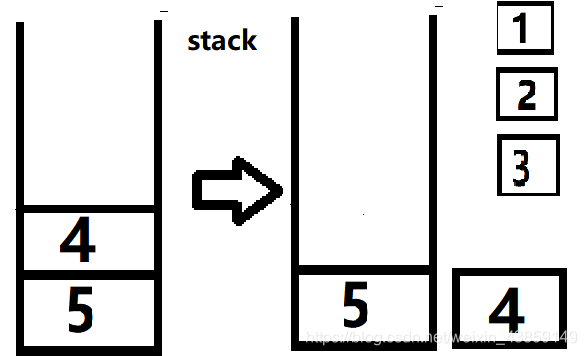 弹出4后,我们就可以把与4相连的6放入栈中,然后进行弹出操作
弹出4后,我们就可以把与4相连的6放入栈中,然后进行弹出操作
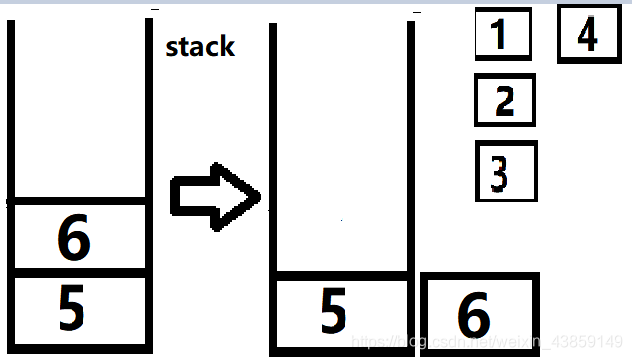 弹出6之后没有数可以放人栈中,我们继续弹出5
弹出6之后没有数可以放人栈中,我们继续弹出5
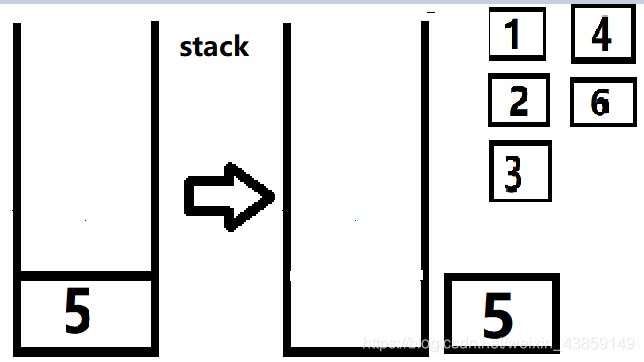
这样我们也得到了结果 1 2 3 4 6 5 说了这么多思想,做的起题才是硬道理,可以试试hdu1010 和hdu 1045 这里以hdu1045举一个例子
Fire Net
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 17270 Accepted Submission(s): 10486
Problem Description Suppose that we have a square city with straight streets. A map of a city is a square board with n rows and n columns, each representing a street or a piece of wall.
A blockhouse is a small castle that has four openings through which to shoot. The four openings are facing North, East, South, and West, respectively. There will be one machine gun shooting through each opening.
Here we assume that a bullet is so powerful that it can run across any distance and destroy a blockhouse on its way. On the other hand, a wall is so strongly built that can stop the bullets.
The goal is to place as many blockhouses in a city as possible so that no two can destroy each other. A configuration of blockhouses is legal provided that no two blockhouses are on the same horizontal row or vertical column in a map unless there is at least one wall separating them. In this problem we will consider small square cities (at most 4x4) that contain walls through which bullets cannot run through.
The following image shows five pictures of the same board. The first picture is the empty board, the second and third pictures show legal configurations, and the fourth and fifth pictures show illegal configurations. For this board, the maximum number of blockhouses in a legal configuration is 5; the second picture shows one way to do it, but there are several other ways.
Your task is to write a program that, given a description of a map, calculates the maximum number of blockhouses that can be placed in the city in a legal configuration.
Input The input file contains one or more map descriptions, followed by a line containing the number 0 that signals the end of the file. Each map description begins with a line containing a positive integer n that is the size of the city; n will be at most 4. The next n lines each describe one row of the map, with a ‘.’ indicating an open space and an uppercase ‘X’ indicating a wall. There are no spaces in the input file.
Output For each test case, output one line containing the maximum number of blockhouses that can be placed in the city in a legal configuration.
Sample Input 4 .X.. …. XX.. …. 2 XX .X 3 .X. X.X .X. 3 … .XX .XX 4 …. …. …. …. 0
Sample Output 5 1 5 2 4
思路:k/n等于行号,k%n等于列号,从0,0点开始搜索,遇到‘.’我们就判断一下他的四周有没有碉堡,如果有那么这个点就不能放碉堡,如果没有那么我们先放一个,然后用递归继续搜索,递归完之后我们又把这个碉堡拆除为下一次搜索做准备。这就是用到了回溯的思想。 附上代码
#include <iostream>
using namespace std;
int n,maxn;
char map1[5][5];
bool judge (int k)
{int i,j;
int r=k/n,c=k%n;
for(i=c;i>=0;i--)
{
if(map1[r][i]=='X')break;
else if(map1[r][i]=='@')return 0;
}
for(i=r;i>=0;i--)
{
if(map1[i][c]=='X')break;
else if(map1[i][c]=='@')return 0;
}
return 1;
}
void dfs(int k,int cnt)
{
int i=k/n,j=k%n;
if(k==n*n)
{
if(cnt>maxn) maxn=cnt;
return ;
}
if(map1[i][j]=='.'&&judge(k))
{
map1[i][j]='@';
dfs(k+1,cnt+1);
map1[i][j]='.';
}
dfs(k+1,cnt);
}
int main()
{
int i;
while(cin>>n)
{if(n==0) break;
maxn=-1;
for(i=0;i<n;i++)
{
cin>>map1[i];
}
dfs(0,0);
cout<<maxn<<endl;
}
return 0;
}
最后作者也比较菜,有错误还望大家能指出,大家可以看看B站大佬正月点灯笼的视频更易懂,附上链接 https://www.bilibili.com/video/av25761720?t=1022

|

|
