单源最短路(dijikstra算法)
百度百科定义中:给定一个带权有向图G=(V,E),其中每条边的权是一个实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径 问题。
dijikstra算法是一种图算法,其中有用到BFS的思想。他和最小生成树有相同之处,但实际解决的是不同的问题。
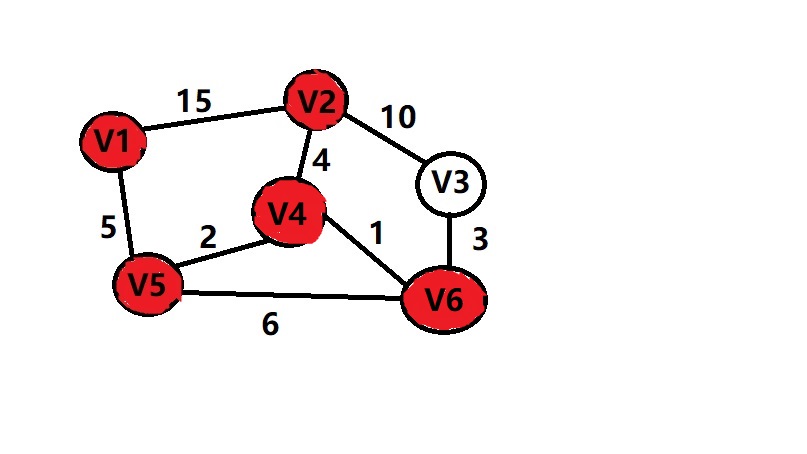
我们还是先看个图 我们假定从V1 出发寻找到 其他各个点的最小的代价,然后在算法程序实现的过程中我们会经常用到优先队列
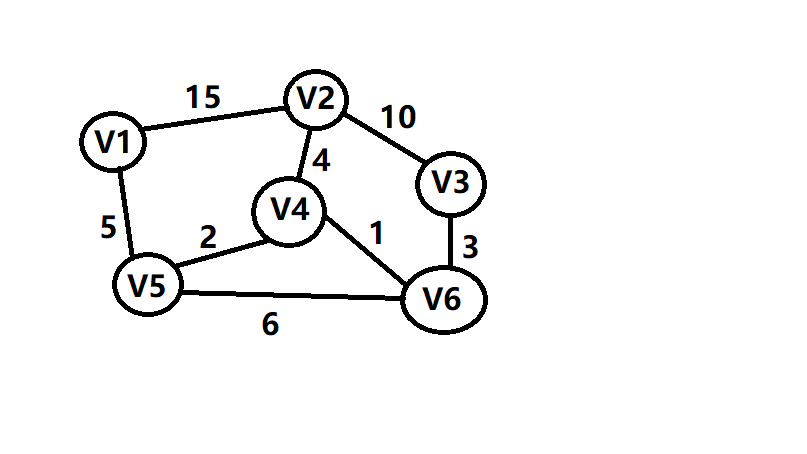
从V1出发 则到V1点的距离为0,表示为(V1,0) vis[V1]=1
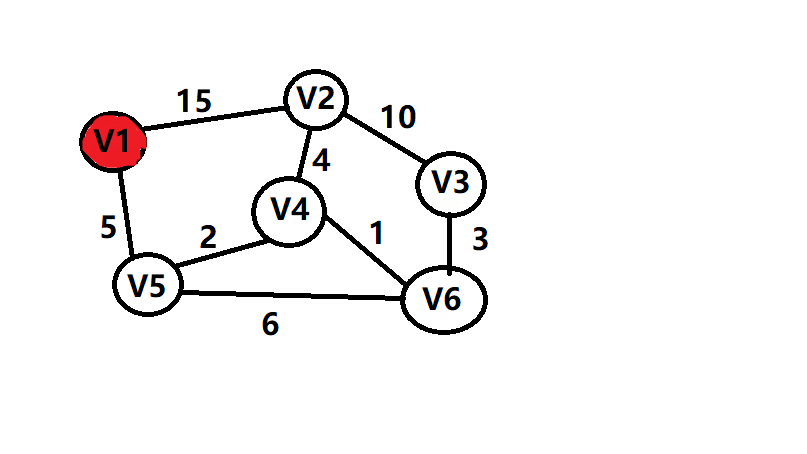

把V1的邻接点放到队列中 (V5,5) ,(V2,15) V5的权重最小所以在优先队列中排在最前面
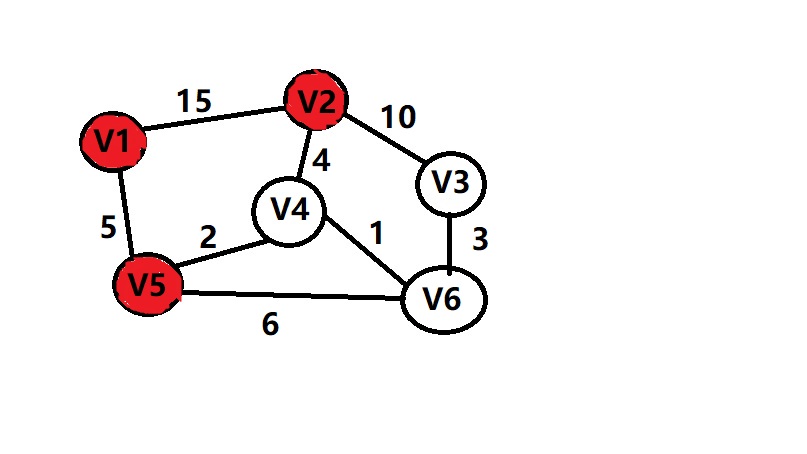
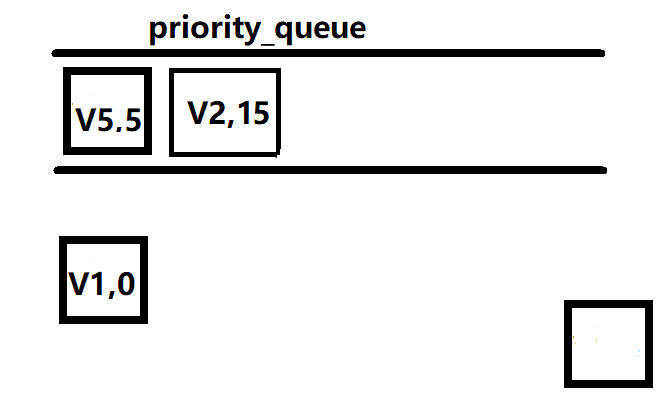
然后弹出队列第一个元素(V5,5) 则V1到V5的距离为5,vis[v5]=1,继续把为V5的邻接点V4,V6放到队列里面(V4,7),(V6,11)
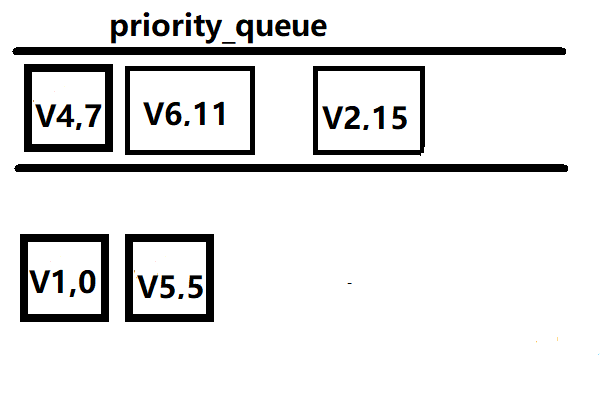
继续弹出V4,vis[V4]=1,把(V2,11) (V6,8)放入优先队列
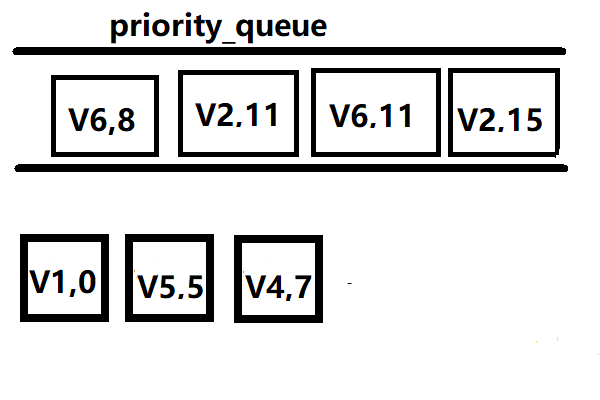
接着弹出(v6,8),vis[V6]=1,放入(v3,11)
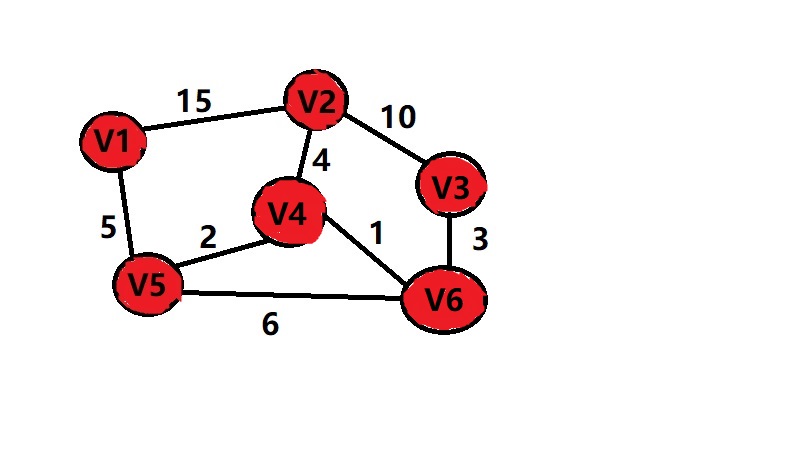
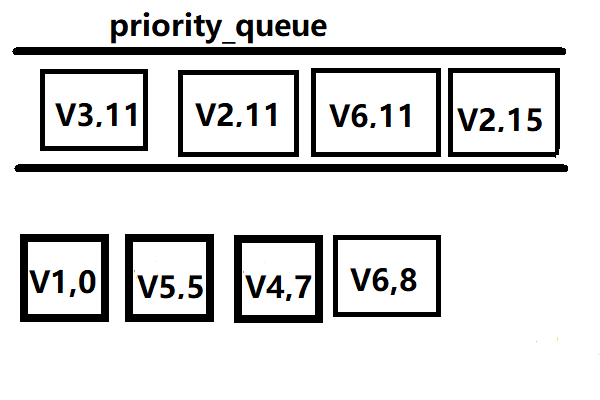
接着弹出(V3,11),vis[V2]=1,放入(v2,21)
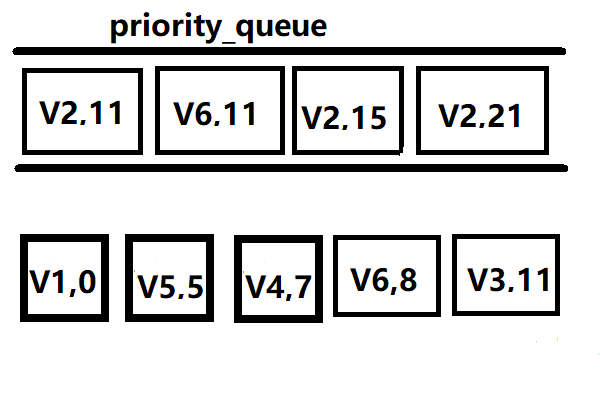
最后弹出(V2,11) vis[V2]=1,到这里从V1出发到所有点的最小代价都算出来了。后面的点由于比原来的距离大所以不用更新。
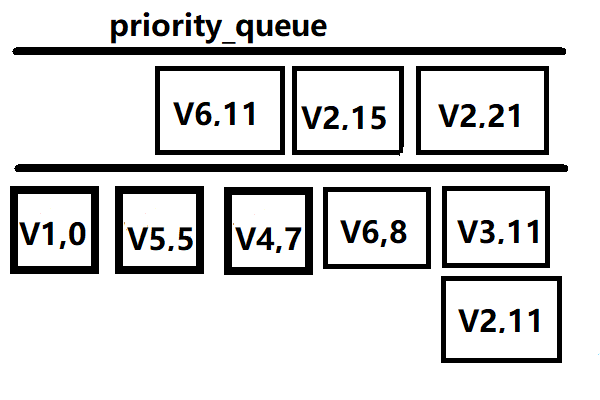
最后我们来做个模板题看看实际的代码实现。
https://www.luogu.org/problem/P4779
题目描述
给定一个 NN 个点,MM 条有向边的带非负权图,请你计算从 SS 出发,到每个点的距离。
数据保证你能从 SS 出发到任意点。
输入格式
第一行为三个正整数 N, M, SN,M,S。 第二行起 MM 行,每行三个非负整数 u_i, v_i, w_iui*,*vi,wi*,表示从 u_i*ui 到 v_ivi* 有一条权值为 w_i*wi 的边。
输出格式
输出一行 NN 个空格分隔的非负整数,表示 SS 到每个点的距离。
输入输出样例
输入 #1
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出 #1
0 2 4 3
给一个大佬的标程
#include <bits/stdc++.h>
using namespace std;
#define INF 0x7fffffff
const int maxn=500010;
struct edge{
int w,to,next;
};
edge e[maxn];
int vis[maxn],dis[maxn],head[maxn];
int n,m,s,cnt;
void add_edge(int u,int v,int d) //链式前向星存图
{
cnt++;
e[cnt].w=d;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;
}
struct node{
int dis;
int pos;
bool operator<(const node &x)const //在优先队列从小到大排序
{
return x.dis<dis;
}
};
priority_queue<node> q; //创建一个优先队列
void dijkstra()
{
node a;
a.dis=0;
a.pos=s;
dis[s]=0;
q.push(a);
while(!q.empty()) //把符号的放入队列 直到队列为空
{
a=q.top();
q.pop();
int x=a.pos,d=a.dis;
if(vis[x]) continue;
vis[x]=1;
for(int i=head[x];i;i=e[i].next) //遍历该点的邻接点
{
int y=e[i].to;
if(dis[y]>dis[x]+e[i].w)
{
dis[y]=dis[x]+e[i].w;
if(!vis[y])
{
q.push((node) {dis[y],y});
}
}
}
}
}
int main()
{
cin>>n>>m>>s;
for(int i=0;i<=n;i++) dis[i]=INF; //把每个距离初始化为无穷大
for(int i=0;i<m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add_edge(a,b,c);
}
dijkstra();
for(int i=1;i<=n;i++)
cout<<dis[i]<<' ';
return 0;
}
笔者能力有限,讲解不到位可以看看大佬讲的思路https://www.bilibili.com/video/av25829980

|

|
