几种排序算法整理及比较
1.冒泡
冒泡排序算法的原理如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
int num[]={5,6,3,4,41,9,16,15,84,5};
for(int i=0;i<10;i++)
{
for(int j=0;j<10;j++)
{
if(num[j]>num[j+1])
swap(num[j],num[j+1]);
}
}
for(int i=0;i<10;i++) cout<<num[i]<<' ';
//结果3 4 5 5 6 9 15 16 32 41
2.选择
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。
int num[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
int n=15;
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
if(num[j]<num[i])
swap(num[i],num[j]);
}
}
for(int i=0;i<n;i++) cout <<num[i]<<' ';
//结果2 3 4 5 15 19 26 27 36 38 44 46 47 48 50
3.希尔排序
希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量 =1,即所有记录放在同一组中进行直接插入排序为止。
增量的选择对排序有较大影响

排序动画过程解释
- 首先,选择增量 gap = 10/2 ,缩小增量继续以 gap = gap/2 的方式
- 初始增量为 gap = 10/2 = 5,整个数组分成了 5 组
- 按颜色划分为【 8 , 3 】,【 9 , 5 】,【 1 , 4 】,【 7 , 6 】,【 2 , 0 】
- 对这分开的 5 组分别使用上节所讲的插入排序
- 结果可以发现,这五组中的相对小元素都被调到前面了
- 缩小增量 gap = 5/2 = 2,整个数组分成了 2 组
- 【 3 , 1 , 0 , 9 , 7 】,【 5 , 6 , 8 , 4 , 2 】
- 对这分开的 2 组分别使用上节所讲的插入排序
- 此时整个数组的有序性是很明显的
- 再缩小增量 gap = 2/2 = 1,整个数组分成了 1 组
- 【 0, 2 , 1 , 4 , 3 , 5 , 7 , 6 , 9 , 0 】
- 此时,只需要对以上数列进行简单的微调,不需要大量的移动操作即可完成整个数组的排序
void ShellSort( ElementType A[], int N )
{ /* 希尔排序 - 用Sedgewick增量序列 */
int Si, D, P, i;
ElementType Tmp;
/* 这里只列出一小部分增量 */
int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
for ( Si=0; Sedgewick[Si]>=N; Si++ )
; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
for ( D=Sedgewick[Si]; D>0; D=Sedgewick[++Si] )
for ( P=D; P<N; P++ ) { /* 插入排序*/
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
4.快速
快速排序(Quicksort)是对冒泡排序的一种改进。基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
void Qsort(int arr[], int low, int high){
if (high <= low) return;
int i = low;
int j = high + 1;
int key = arr[low];
while (true)
{
/*从左向右找比key大的值*/
while (arr[++i] < key)
{
if (i == high){
break;
}
}
/*从右向左找比key小的值*/
while (arr[--j] > key)
{
if (j == low){
break;
}
}
if (i >= j) break;
/*交换i,j对应的值*/
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/*中枢值与j对应值交换*/
int temp = arr[low];
arr[low] = arr[j];
arr[j] = temp;
Qsort(arr, low, j - 1);
Qsort(arr, j + 1, high);
}
5.堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆最核心也是最基本的操作只有两个,即插入和删除,其它操作都属于扩展操作。堆的操作要满足结构性和堆序性才能结束,比如,在堆的最后插入了一个新的节点,该节点值小于其父节点的值,则需要将该节点与父节点交换,循环此过程,直到重新满足堆序性为止。我们以小顶堆为例,采用图解的方式来讲解堆的插入和删除操作。

void max_heapify(int arr[], int start, int end)
{
//建立父节点指标和子节点指标
int dad = start;
int son = dad * 2 + 1;
while (son <= end) //若子节点指标在范围内才做比较
{
if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两个子节点大小,选择最大的
son++;
if (arr[dad] > arr[son]) //如果父节点大於子节点代表调整完毕,直接跳出函数
return;
else //否则交换父子内容再继续子节点和孙节点比较
{
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len)
{
//初始化,i从最後一个父节点开始调整
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
//先将第一个元素和已经排好的元素前一位做交换,再从新调整(刚调整的元素之前的元素),直到排序完毕
for (int i = len - 1; i > 0; i--)
{
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}
几种算法的比较
稳定性上:
选择排序、希尔排序、快速排序、堆排序是不稳定的
冒泡是稳定的
时间复杂度上:
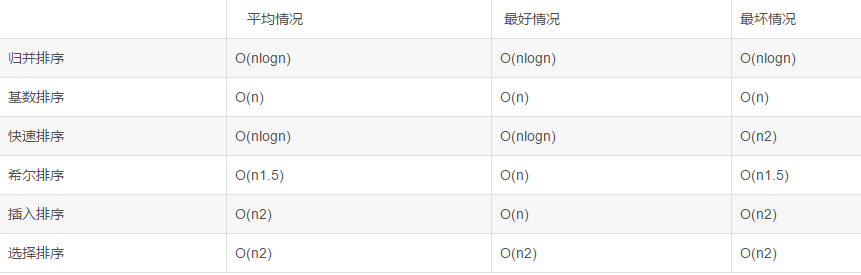

|

|